Nu har jag smygläst den här tråden alldeles för länge utan att skriva något. Som ni kan se har jag gjort en friläggning, lik Bearings friläggning.
Vi vill maximera hastigheten i kurvan. Den radiella rörelseekvationen (1) ger oss hastigheten. Momentekvation (2) kring däckets kontaktpunkt ger ett uttryck för alfa. Detta sätts in i ekv. 1. Vi får då "v" på båda sidor likhetstecknet, men det löser datorn snabbt med ett par iterationer.
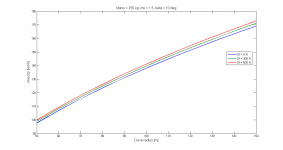
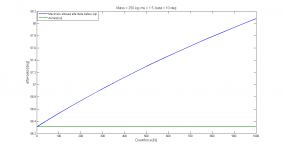
Nummer 3 är funktionen man vill maximera för att öka hastigheten och den har jag plottat separat.
Säg till om något är fel i mina ekvationer så fixar jag nya grafer. Märker dock nu att för beta = 0 får jag ingen hastighetsskillnad när jag ändrar på downforcen, vilket man ju borde få enligt ekvationerna man får då man ställer upp jämvikt med beta = 0. Skulle kunna vara fel i koden också.
EDIT:Glömde bifoga bild på friläggning.
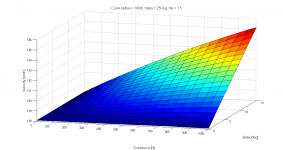
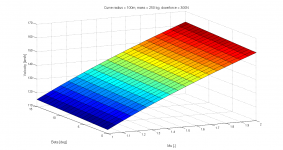

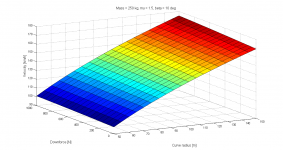
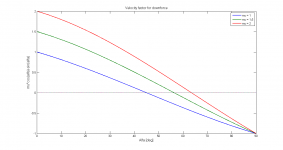

Vi vill maximera hastigheten i kurvan. Den radiella rörelseekvationen (1) ger oss hastigheten. Momentekvation (2) kring däckets kontaktpunkt ger ett uttryck för alfa. Detta sätts in i ekv. 1. Vi får då "v" på båda sidor likhetstecknet, men det löser datorn snabbt med ett par iterationer.
Nummer 3 är funktionen man vill maximera för att öka hastigheten och den har jag plottat separat.
Säg till om något är fel i mina ekvationer så fixar jag nya grafer. Märker dock nu att för beta = 0 får jag ingen hastighetsskillnad när jag ändrar på downforcen, vilket man ju borde få enligt ekvationerna man får då man ställer upp jämvikt med beta = 0. Skulle kunna vara fel i koden också.
EDIT:Glömde bifoga bild på friläggning.








Last edited:

 (fina grafer av Svenne100, jag har dock inte kollat noggrant på dom ännu)
(fina grafer av Svenne100, jag har dock inte kollat noggrant på dom ännu)








