Downforce på hojar

[RandomDude]

Precis, om vingen verkligen alltid ger ett positivt bidrag så är det alltså bättre desto större kraft vingen ger och vi kan därmed sätta vingens kraft till >> massan hos ekipaget.

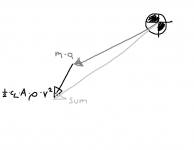
Då kan man sedan förenkla förståelsen genom att och man sätter man ekipagets vikt = noll och tittar bara på kraften, F från vingen vid olika nedläggningsvinklar, alfa och däckens friktion, u mot underlaget.

Kraften neråt blir då:
F*sin(alfa)
Kraften radiellt blir:
u*F*sin(alfa) - F*cos(alfa)

Det är alltså uppenbart att vi har två motverkande krafter och sinusfunktionens natur gör att det alltid finns en vinkel där summan av krafterna kommer byta tecken och bli negativ. dvs vingen ger då ett nagativt bidrag.

Nu vet jag inte hur du definierar vinkeln alfa, men om alfa = lutningsvinkeln (0 om man kör rakt fram), så blir formeln:
Normalkraft vinge:
Fn = Fvinge*cos(alfa)
Kraften i radiell led för enbart vingen blir:
Fr = Fvinge*sin(alfa)

Om vi bortser från aerodynamik och motorcykeln håller en lutning på 64 grader och föraren håller en lutning på ca 70 grader (föraren hänger ut) så kan vi anta att den gemensamma effektiva lutningen av hela ekipaget blir ca 67 grader. Alltså friktionskoefficient mellan däck och mark tillåter att kraften appliceras med upp till 67 grader utan att tappa greppet.

Om nu vingens kraft appliceras i en vinkel av 64 grader (3 grader mindre än vad däcken klarar) så betyder det att det då finns potential att luta ekipaget lite mer (motsvarande vingens kraft för 3 graders vinkel).

Det jag försöker säga är att övergången till där vingens effekt är negativ sker inte vid 45 grader, det skulle den göra om friktionskoefficienten var exakt 1.0. Men eftersom friktionskoefficienten är mycket högre än 1.0 så sker denna övergång någonstans runt 67 grader, den vinkel där hojen+förare klarar att köra utan vingar.

 

[Josef]

Jag tror vi hamnat nåååågot över nivån satt i trådstarten.
Det man kan tillägga om downforce vid kurvtagning i RR är att även om rörliga aerodynamiska hjälpmedel på hojen är förbjudna så utgör både marken och föraren rörliga delar av det aerodynamiska paketet.
Jag skulle bli storligen förvånad om man inte tar hänsyn till detta vid utvecklingen av MotoGP-maskiner även om det gissningsvis handlar mer om att undvika lyft och instabilitet snarare än att skapa massor av downforce.

 

[Two stroke man]

Vinkeln på hojen beror på hur mycket du hänger av. Hojen kam vara mycket mer upprätt om man hänger ut mycket som Bearing syftar på och vinkeln på hojen har stor inverkan på aerodynamiken. Allltså vingarna på hojen kan ge effektiv downforce i en kurva men bara om föraren hänger ut.

Dessutom ser jag att både yamaha och ducati jar vingar som lutar snett nedåt. Alltså om förarens ben kan blocker luftströmmen över vingen på insidan av kurvan (som lutar år "fel" håll) så skulle vinge på utsidan med mer gynnsam vinkel dominera downforcen.

Du krånglar till det och gör det bara svårare för dig själv och alla andra.

Skit i förarens positon det intressanta är om vingen ger positiv eller negativ effekt så det bara kraftkomposanterna som ges av vingen vi som söker.

 

[Two stroke man]

Nu vet jag inte hur du definierar vinkeln alfa, men om alfa = lutningsvinkeln (0 om man kör rakt fram), så blir formeln:
Normalkraft vinge:
Fn = Fvinge*cos(alfa)
Kraften i radiell led för enbart vingen blir:
Fr = Fvinge*sin(alfa)

Du har rätt, jag kastade om sinus och cosinus.
Editerar mitt inlägg nu.

 

[Two stroke man]

Jag sa 45 grader tidigare men det gäller egentligen bara om man approximerar friktionen till =1 så dessa 45 grader är inte en exakt siffra.

Jag har dock funderat ytterligare lite på Rossis vingar för luften under hojen kommer bromsas upp och passera hojen med lägre fart än luften som passerar över hojen och därmed kommer den övre vingen ge ett kraftigare bidrag än den undre vingen.
Så jag måste nog ändå revidera mina åsikter och säga att rätt utformade vingar kanske ändå kan ge positivt bidrag.

(Skriver att luften bromsas upp eftersom det ur aerodynamisk synvinkel är enklare att betrakta MC som stillastående och bara studera luftens rörelse relativt MC.)

 

[R2]

Väldigt få vet ju med säkerhet varför man i motogp använder vingar och vilka effekter man dels efterfrågar och dels får.
Det man utanför denna kretsen tycks vara överens om är att ducatis vingar håller ner framhjulet på rakor och och vid milda nerläggningsvinklar, den positiva effekten av detta är att man kan ställa ner hur mycket wheeliekontrollen griper in vilket i sin tur ger mer effekt i backen.


Sen vill jag framföra min tanke att vingarna vid fullt nerlägg, som en del här säger, verkar i linje med hojen, inte ner mot backen..
Men det är väl för fanken just det man vill för bättre grepp!?
Verkan av jordens gravitation när Lorenzo tar en kurva i 180blås är närmast försumbar jämfört med hojens centrifugalkraft i linje med hojen.

Dessutom skulle en större downforce inte funka ihop med däcken som inte är gjorda för´t.

Avslutar med en bild på första hojen John Britten byggde, Aero D-zero.
Här va teorin tvärtemot det jag säger ovan, att man behövde kraften rakt ner,
och detta med två vinklade vingar skötte sig själv eftersom föraren hänger av hojen inåt och då förstör luftflödet bakom den vinge som skulle trycka hojen "åt sidan".

Att vingarna på Rossis hoj hade en inbördes vinkel beror nog hur dom vill ha luftflödet runt hojen.
Och ja kåpor har en viss downforce om konstruktören eftersträvat det.
Kul ämne detta.

 

[Ese]

Som Josef säger är rörliga aerodynamiska hjälpmedel förbjudna i RR.
-men för gatubruk, OM man ville bygga nåt för downforce som faktiskt hjälper vid kurvtagningen, skulle det vara en liten vinge utan magkåpan. Motordriven, automatiskt styrt (g-kraftsensor styrt?).
-> man vill generera bara normalkraft dvs rakt ner mot marken, och så nära till däckens marklinje som möjligt så att det inte blir en ny kraftpar som försöker "tippa hojen".

 

[Bearing]

Ok, du försöker alltså nu argumentera fram att:
0.9 = sin(64) < friktionen * sin(64) = 0.44*friktionen.

Om man bortser från aerodynamik är som sagt maximal lutningsvinkel (d.v.s vinkeln på accelerationskraftvektorn från lodrätt) invers tangens av friktionskoefficienten. 55° kräver friktionskoefficienten 1,4. 60° kräver friktionskoefficienten 1,7. 65° kräver friktionskoefficienten 2,1. Så man kan ju konstatera att dom kör med rätt klibbiga däck / abrasiv asfalt i MotoGP.

Om du/någon önskar kan jag kan rita en bild med alla vektorer, där det blir tydligt att så fort vingens vektor pekar mer ned mot asfalten, än accelerationens vektor, hjälper vingen.

 

[Two stroke man]

Som Josef säger är rörliga aerodynamiska hjälpmedel förbjudna i RR.
-men för gatubruk, OM man ville bygga nåt för downforce som faktiskt hjälper vid kurvtagningen, skulle det vara en liten vinge utan magkåpan. Motordriven, automatiskt styrt (g-kraftsensor styrt?).
-> man vill generera bara normalkraft dvs rakt ner mot marken, och så nära till däckens marklinje som möjligt så att det inte blir en ny kraftpar som försöker "tippa hojen".

Jag skulle nog bygga två vingar som ett stor V sett framifrån och dessa ska kunna vridas i nederkant så att attackvinkeln ändras.

Då kan i kurvan den "nedre" vingen ha attackvinkel för att pressa ner hojen mot marken och den "övre" vinken kan ha attackvinkel som trycker hojen inåt i kurvans radie som ett flygplan.

Och vid inbromsning kan de vridas så att man får luftbroms.

Hej, vad fort det skulle gå med 5g i kurvorna.

 

[Two stroke man]

Om man bortser från aerodynamik är som sagt maximal lutningsvinkel (d.v.s vinkeln på accelerationskraftvektorn från lodrätt) invers tangens av friktionskoefficienten. 55° kräver friktionskoefficienten 1,4. 60° kräver friktionskoefficienten 1,7. 65° kräver friktionskoefficienten 2,1. Så man kan ju konstatera att dom kör med rätt klibbiga däck / abrasiv asfalt i MotoGP.

Om du/någon önskar kan jag kan rita en bild med alla vektorer, där det blir tydligt att så fort vingens vektor pekar mer ned mot asfalten, än accelerationens vektor, hjälper vingen.

Insåg också det där med friktionen när jag ställde upp ekvationen, ganska sjukt faktiskt.

Ja, om du fortfarande inte insett att det är dåligt när kraftvektorn pekar allt för mycket utåt i periferin så är det nog dags att du ritar upp de där kraftvektorerna.

 

[Ese]

Man vill ju minska luftmotståndet i alla möjliga lägen (trots så att man inte genererar upforce). Bara under tiden man vill ha downforce skulle då vara "tillåtet" att öka luftmotstånd. Två vingar som syns framifrån låter som att de skulle ha "större" påverkan på hojens Cw och Areaprojektionen sedd framifrån...

--
Edit: 5g i kurverna skulle vara skojigt i kurverna "vid en elak s*uthäng"..

 

[Josef]

Jag skulle nog bygga två vingar som ett stor V sett framifrån och dessa ska kunna vridas i nederkant så att attackvinkeln ändras.

Då kan i kurvan den "nedre" vingen ha attackvinkel för att pressa ner hojen mot marken och den "övre" vinken kan ha attackvinkel som trycker hojen inåt i kurvans radie som ett flygplan.

Den nedre vingen kan ju med tillräcklig rörlighet fungera som en splitter på en bil och med rörliga kjolar på magkåpan som håller hojen fastsugen mot backen kan man nog få rätt bra downforce. Verkar vara värt att bygga på en gathoj.

 

[RandomDude]

Du krånglar till det och gör det bara svårare för dig själv och alla andra.

Skit i förarens positon det intressanta är om vingen ger positiv eller negativ effekt så det bara kraftkomposanterna som ges av vingen vi som söker.

Förarens position avgör om vingen har en positiv eller negativ effekt.

Vi tar extremfallet när en mycket tung förare burkar så in i tusan, då är hojen helt upprätt genom kurvan (lutningsvinkeln = 0) medans hans kropp håller en lutning på 80-90 grader. I det fallet är ju vingar på hojen mycket gynnsamma då de enbart ger ökad normalkraft rakt ner i marken. Det andra extremfallet är när föraren burkar åt fel håll, då lutar motorcykeln 80-90 grader för att göra samma sväng, då är vingar på hojen mycket dåliga att ha.

Nu kom vi fram till att övergången där vingar är dåliga/bra sker vid ca. 67 graders lutningsvinkel. Alltså om föraren genom att burka kan få hojen att luta mindre än 67 grader så är det positivt att ha vingar, om föraren lutar åt fel håll så att hojen lutar mer än 67 grader så är det negativt att ha vingar.

 

[RandomDude]

Jag gjorde en snabb överslagsräkning baserad på att vingen skulle ge 50 kg kraft (gissning) i samma vinkel som motorcykeln och att motorcykeln lutar 64 grader medans ekipaget med förare (hoj+förare = 200 kg) lutar tillsammans 67 grader. Då skulle friktionskoefficienten mellan däck/mark kunna vara 2.8 % lägre än om man inte hade vinge (alltså vingen skulle ge en effekt av att däcken har 2.8 % bättre grepp).

 

[Ese]

Hoj + förare med totalvikt 200kg är lite underkant för en hygglig SH + vuxen förare med BMI 22

Men PONERA att det finns en vägböj som kallas fotokurvan, och föraren kan under normalt väglag rulla genom kurvan med hastighet 105km/h. Hela friktionsbudgeten använder man då att vinna centrifugalkraft (mvv/r), inget finns kvar för att bromsa eller acca.
Sen PONERAR vi också att mha en ny vinge kan man generera 50kg Downforce, rakt ner (realistiskt med 105km/h). Med downforce men annars samma förutsättningar kan man köra genom kurvan ca 1.12 gånger snabbare, dvs ca 117 km/h.
(Förhållande vDmax/vmax = SQR(1+FDown/mg))

-vill nu också sluta för min del med kommentar att med nya vingar man vill inte införa nya krafter/kraftpar i hojen som påverkar körbarhet och stabilitet. T.ex magvinge + uppvinge kunde i värsta fall leda till att föraren måste balansera med kroppen åt "felt" håll..

 

[Ulvhamne]

Förarens position avgör om vingen har en positiv eller negativ effekt.

Vi tar extremfallet när en mycket tung förare burkar så in i tusan, då är hojen helt upprätt genom kurvan (lutningsvinkeln = 0) medans hans kropp håller en lutning på 80-90 grader. I det fallet är ju vingar på hojen mycket gynnsamma då de enbart ger ökad normalkraft rakt ner i marken. Det andra extremfallet är när föraren burkar åt fel håll, då lutar motorcykeln 80-90 grader för att göra samma sväng, då är vingar på hojen mycket dåliga att ha.

Nu kom vi fram till att övergången där vingar är dåliga/bra sker vid ca. 67 graders lutningsvinkel. Alltså om föraren genom att burka kan få hojen att luta mindre än 67 grader så är det positivt att ha vingar, om föraren lutar åt fel håll så att hojen lutar mer än 67 grader så är det negativt att ha vingar.

Med tanke på att man i princip behöver sitta på en motoGPhoj för att kunna lägga ner 67 grader (inte ens de kan väl komma ner riktigt så långt iofs) och stanna kvar på asfalten så är ju förarens avhäng irrelevant redan där.

https://www.youtube.com/watch?v=J73XRDGPcpE

 

[Bearing]

Det går väl inte att sätta ett absolutbelopp på vinkeln där vingen slutar hjälpa?
Vinkeln där vingen hjälper är väl endast relativ accelerationens vinkel?
D.v.s om vingen vinklas mer ned i backen än accelerationen, hjälper den. Vilket i praktiken har med åt vilket håll föraren hänger ut (som sagt).

 

[Bearing]

Ja, om du fortfarande inte insett att det är dåligt när kraftvektorn pekar allt för mycket utåt i periferin så är det nog dags att du ritar upp de där kraftvektorerna.

Kommentar till bilden?

 

[Two stroke man]

Kommentar till bilden?

Ja, men jag har inte tid att rita och utveckla det vidare just nu.

Det korta svaret är att du inte har en komplett jämnviktsekvation där.

 

[Bearing]

Ja, men jag har inte tid att rita och utveckla det vidare just nu.

Det korta svaret är att du inte har en komplett jämnviktsekvation där.

Jo, jag vet att det inte är en komplett jämviktsekvation. Men det är väl inte heller jämvikt, då motorcykeln accelererar i sidled.

Ritade den bild jag haft i huvudet, som innehåller "centrifugalkraften". Men blir det verkligen någon skillnad vad gäller detta, av att rita upp alla krafter och reaktionskrafter?