Downforce på hojar

[Two stroke man]

Jo, jag vet att det inte är en komplett jämviktsekvation. Men det är väl inte heller jämvikt, då motorcykeln accelererar i sidled.

Ritade den bild jag haft i huvudet, som innehåller "centrifugalkraften". Men blir det verkligen någon skillnad vad gäller detta, av att rita upp alla krafter och reaktionskrafter?

Ja, det blir fullständig jämvikt eftersom centrifugalkraften är en acceleration och F = m*a.

Och det är händelsevis denna acceleration du vill maximera.

 

[Bearing]

Jo, det är väl självklart att man vill maximera sidoaccelerationen.

Men jag menar att om man frilägger motorcykeln kommer summan av krafterna inte bli noll. Summan blir noll i lodrät riktning. Men i horisontell riktning blir ju summan inte noll, för då skulle motorcykeln åka rakt fram.

Jag försökte mig på en komplett friläggning från början. Men när jag blev osäker så nöjde jag mig med den förenklade bilden, då jag tror att den ändå visar vingens påverkan korrekt.

 

[Two stroke man]

Jo, det är väl självklart att man vill maximera sidoaccelerationen.

Men jag menar att om man frilägger motorcykeln kommer summan av krafterna inte bli noll. Summan blir noll i lodrät riktning. Men i horisontell riktning blir ju summan inte noll, för då skulle motorcykeln åka rakt fram.

Jag försökte mig på en komplett friläggning från början. Men när jag blev osäker så nöjde jag mig med den förenklade bilden, då jag tror att den ändå visar vingens påverkan korrekt.

Vi tar det steg för steg och börjar utan vinge på hojen. Vad är då maximal sidoacceleration?
Är vi överens om att maximal sidokraft då blir, Fmax = u*m*g?

Maximal sidoacceleration, a,max = Fmax/m = (u*m*g)/m?

 

[Two stroke man]

Jo, det är väl självklart att man vill maximera sidoaccelerationen.

Men jag menar att om man frilägger motorcykeln kommer summan av krafterna inte bli noll. Summan blir noll i lodrät riktning. Men i horisontell riktning blir ju summan inte noll, för då skulle motorcykeln åka rakt fram.

Jag försökte mig på en komplett friläggning från början. Men när jag blev osäker så nöjde jag mig med den förenklade bilden, då jag tror att den ändå visar vingens påverkan korrekt.

Vidare så tror jag vi är överens om att vinge ger dessa krafter?

 

[Boost 3]

Äh va fan vad ni krånglar till det ,,,de e ju bara dricka RedBull

 

[RandomDude]

Vidare så tror jag vi är överens om att vinge ger dessa krafter?

Jo det är helt korrekt. Sedan vad friktionstalet "u" representerar är ju hur mycket mer sidoacceleration däcken klarar jämfört med accelerationen ned mot marken. Om vi antar u = 2.1 för motogp däck på bana så klarar däcken 2.1 gånger så hög sidoacceleration jämfört med kraften rakt ned mot marken.

Alltså är vingen gynnsam så länge som (Fvinge*sin(alfa)) / (Fvinge*cos(alfa)) är mindre än 2.1 (vilket sker om alfa är mindre än 65 grader). Så om föraren lyckas hålla hojen lite mer upprätt än 65 grader genom att hänga ut med kroppen så är vingen gynnsam att använda (vingens sidokraft är mindre än 2 gånger nedåtkraften).

 

[Bearing]

Vi tar det steg för steg och börjar utan vinge på hojen. Vad är då maximal sidoacceleration?
Är vi överens om att maximal sidokraft då blir, Fmax = u*m*g?

Maximal sidoacceleration, a,max = Fmax/m = (u*m*g)/m?

Ja, helt överens. Även när det gäller den andra bilden.

 

[Fläppen1]

Om man tänker sig två ytterligheter, den ena att man låter hojen stå vertikalt i svängen (hänga massor ) och den andra att man inte hänger alls. Utan att ha satt mig ner och ritat och räknat känns det som om man har max hjälp av aerodynamisk downforce i det första fallet och ingen hjälp alls i det andra fallet. Det första fallet kan jämföras en bil och bilar har ju glädje av aerodynamisk downforce i kurvor. Det andra fallet med ett hojekipage som bara blivit lite tyngre. Någonstans mittemellan dessa båda ytterligheter är man ju och har alltså nytta av vingar i kurvor.

 

[Two stroke man]

Ja, helt överens. Även när det gäller den andra bilden.

Bara att summera dom då.

- - - Updated - - -

Ja, helt överens. Även när det gäller den andra bilden.

Bara att summera dom då.

 

[Bearing]

Bara att summera dom då.

Jag ser inte hur summeringen stärker din tes.

Reaktionskrafterna och friktionskrafterna i marken kommer väl se ut som min bild, men roterade 180°.

För att lösa ekvationen behöver det vara känt var vingen är placerad i förhållande till tyngdpunkten och kontaktpunkten med marken.

Ett sätt att lösa ekvationen är att lösa momentekvationen kring tyngdpunkten. Utan att införa siffror kan man ju resonera lite. Givet är att vingen sitter i centrum av motorcykeln, d.v.s till vänster om tyngdpunkten, förutsatt att föraren burkar. Det betyder att vingen vill vrida tyngdpunkten moturs. För att motverka det momentet måste alltså någon annan kraft verka för att vrida tyngdpunkten medurs. Den enda tillgängliga kraften är kraften från vägen. Den måste peka en aning till vänster om tyngdpunkten. Det innebär att vinkeln jämfört med vinglöst är lägre. Lägre vinkel innebär att det krävs lägre friktion för att hålla jämvikt. D.v.s det går att köra fortare/med större lutning, innan däcken tappar fästet.

Eller tänker jag fel?

 

[Bearing]

Angående lutningsvinkel, kom jag att tänka på en sak. Däcken har ju bredd och profil. Det innebär ju att det krävs mer lutning för att åstadkomma en viss vinkel mellan kontaktpunkten och tyngdpunkten. Så friktionskoefficienten är inte över 2. Men den lär vara nära 1,5 i alla fall.

 

[Two stroke man]

Jag ser inte hur summeringen stärker din tes.

Reaktionskrafterna och friktionskrafterna i marken kommer väl se ut som min bild, men roterade 180°.

För att lösa ekvationen behöver det vara känt var vingen är placerad i förhållande till tyngdpunkten och kontaktpunkten med marken.

Ett sätt att lösa ekvationen är att lösa momentekvationen kring tyngdpunkten. Utan att införa siffror kan man ju resonera lite. Givet är att vingen sitter i centrum av motorcykeln, d.v.s till vänster om tyngdpunkten, förutsatt att föraren burkar. Det betyder att vingen vill vrida tyngdpunkten moturs. För att motverka det momentet måste alltså någon annan kraft verka för att vrida tyngdpunkten medurs. Den enda tillgängliga kraften är kraften från vägen. Den måste peka en aning till vänster om tyngdpunkten. Det innebär att vinkeln jämfört med vinglöst är lägre. Lägre vinkel innebär att det krävs lägre friktion för att hålla jämvikt. D.v.s det går att köra fortare/med större lutning, innan däcken tappar fästet.

Eller tänker jag fel?

Ja, du tänker fel och du behöver inget mer information för att ta fram krafterna. Det är fysik på gymnasienivå.

Och du har flera steg i förståelse kvar innan du är mogen för siffror till ekvationerna.

 

[Two stroke man]

Angående lutningsvinkel, kom jag att tänka på en sak. Däcken har ju bredd och profil. Det innebär ju att det krävs mer lutning för att åstadkomma en viss vinkel mellan kontaktpunkten och tyngdpunkten. Så friktionskoefficienten är inte över 2. Men den lär vara nära 1,5 i alla fall.

Du krånglar till det så att du går vilse i dina egna tankar.

 

[Bearing]

Ja, du tänker fel och du behöver inget mer information för att ta fram krafterna. Det är fysik på gymnasienivå.

Och du har flera steg i förståelse kvar innan du är mogen för siffror till ekvationerna.

Jag gjorde sådana här saker på gymnasiet, det stämmer. Jag har inte räknat på sånt här på 15 år. Men det är ju som du säger, väldigt enkelt. Dock är jag inte helt tvärsäker, just eftersom att det var länge sedan.

Jag tror att du har fel angående att det inte skulle behövas mer information för att lösa ut krafterna. Eftersom att det är du som påstår att inte mer information krävs, föreslår jag att du löser ekvationen.

Anledningen till att jag inte sätter in siffror är att det skulle behövas så många antaganden. Jag ansåg att ett resonemang skulle visa poängen på ett mer pedagogiskt sätt. Men det verkar som att jag gjorde en felbedömning.

Från min sida har det varit så uppenbart att du haft fel hela tiden, att jag försöker vara ödmjuk, och visa att det här inte var så lätt och självklart för mig heller. Så att du inte ska se allt för dålig ut i den här diskussionen. Men jag tror att, eftersom att du nu börjar spekulera i hur "mogen" jag är, hade det varit bättre att köra hårt, och inte visa någon hänsyn.

 

[Bearing]

Du krånglar till det så att du går vilse i dina egna tankar.

Med det uttalandet kan jag inte börja tro annat än att du med avsikt försöker föra in mig i en diskussion utan större syfte, förutom ditt eget nöje. D.v.s "trolla".

Självklart behöver en motorcykel med breda hjul, som förflyttar kontaktpunkten omkring 100mm bort från centerlinjen, och 100mm i höjdled, luta mer, för att få önskad vinkel mellan kontaktpunkten och tyngdpunkten, än om hjulet hade varit en skiva med 1mm bredd. Förarens burkning minskar lutningen en aning, men lutningen är nog ändå högre, än i fallet med skivan som hjul. Och detta har betydelse för hela resonemanget med vingen.

 

[Two stroke man]

Bearing, Om du som är så ödmjuk skulle orka räkna lika flitigt som du orkar knappra på tangentbordet så tror jag inte vi skulle vara här.

Jag gör väl ekvationen åt dig också då, krafter på hojen.

Krafter ner mot asfalten, Fy och vingens kraft, Fv.
Fy = mg + Fv*cos(alfa)

Krafter som trycker hojen in mot kurvans radie
Fr = u*Fy - Fv*sin(alfa)
eller:
Fr = u*(mg + Fv*cos(alfa)) - Fv*sin(alfa)

Vidare vill vi maximera accelerationen, a in mot kurvans radie, dvs

a = Fr/m = umg/m +uFv/m*cos(alfa) - Fv/m*sin(alfa)

Jag har delat upp det för och visa att motorcykelns massa samt lutning inte påverkar kurvtagningsförmågan vid fallet utan vinge. Det är alltså endast vingens lutning som är av intresse.

Här har du alltså den ekvation som du vill maximera.

a = ug +uFv/m*cos(alfa) - Fv/m*sin(alfa)


Sätt in vilka siffror du vill men förslagsvis bör du titta på extremfallen, dvs alfa = 0 respektive alfa = 90 grader.
Om det är bra med en vinge så bör det rimligtvis vara så att en extremt kraftig vinge är ännu bättre och vi kan för intuitionens skulle fundera på extremfallet med en otroligt kraftfull vinge som ger en kraft på 1000000 och en lätt MC eller säg en cykel på 15 kg med 85 kg förare.
Och du kan sätta g = 10 för enkelhetens skull.

Då får vi denna
a = u*10 +u*10000*cos(alfa) - 10000*sin(alfa)

Jag gjorde alltså vingens kraft så kraftfull att vi kan förenkla ekvationen till

a = 10000*( u*cos(alfa) - sin(alfa))

Vid det ena extremfallet är alfa = 0 och ekvationen blir

a = 10000*u m/s^2

Det andra extremfallet är att alfa = 90 och blir då

a = - 10000 m/s^2

Notera minustecknet här

Sätter du friktionen u = 1 så har du en funktion som byter tecken och blir negativ vid alfa = 45.

 

[Two stroke man]

En MC utan down force kan alltså svänga med accelerationen u*g så skillnaden på en hoj med down force respektive utan blir

deltaa = ug +uFv/m*cos(alfa) - Fv/m*sin(alfa) - ug

deltaa= Fv/m*(u*cos(alfa) - *sin(alfa))

Fy/m är ju bara en konstant så därmed kvarstår ekvationen som definierar vingens funktion.

f(u,alfa) = u*cos(alfa) - sin(alfa)

Det är en ekvation som för alla u<2 förr eller senare byter tecken och blir negativ och pga sinuskurvas utseende krävs det u väldigt nära 2 för att funktionen ska vara positiv ända upp till 64 grader som gphojen kunde lutas.

 

[RandomDude]

Det är en ekvation som för alla u<2 förr eller senare byter tecken och blir negativ och pga sinuskurvas utseende krävs det u väldigt nära 2 för att funktionen ska vara positiv ända upp till 64 grader som gphojen kunde lutas.

Bra härledning av alla krafter. Alltså vingen har minimal betydelse i kurvor, eventuellt en mycket liten positiv effekt eftersom hojen och där med vingen är mer aningen mer upprätt än totala lutningen av hoj+förare.

Så antagligen stämmer Ducatis uttalande om att vingens syfte är för att minska wheelies på rakorna då de har gott om effekt och endast är begränsade av att framhjulet lyfter.

 

[Bearing]

Verkar ju vara något missförstånd här.

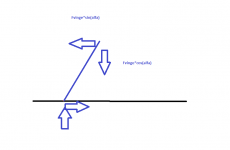
"f(u,alfa) = u*cos(alfa) - sin(alfa)"
Om vi sätter f(u,alfa) = 0, där övergången mellan hjälp och stjälp sker, får vi u = tan(alpha)
Vilket är samma formel som maximal lutningsvinkel med gravitation, utan vinge.

Tyngdpunktens vinkel och vingens vinkel (som verkar i motorcykeln centerlinje) har ju ett förhållande. Jag har ju inte sagt att vingen hjälper för alla vinklar, utan endast för vinklar som är lägre än tyngdpunktens vinkel. Eftersom att tyngdpunktens vinkel är begränsad av friktionen, vet vi ju redan innan, att vingens vinkel är lägre än vinkeln där den slutar hjälpa. (Om vi bortser från däckets bredd. Tar vi med det tror jag hela mitt resonemang faller i praktiken.)

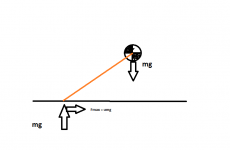
Din uträkning tar inte i beaktande att tyngdpunkten måste ligga innanför kontaktpunkten med asfalten, och producera ett moment som balanserar accelerationskraften i sidled. Om vingen producerar en kraft som är många storleksordningar större än m*g, kommer motorcykeln ändå inte kunna kör avsevärt fortare i kurvan*. Extremfallet, där m*g kan försummas, d.v.s motorcykeln kan anses vara bara vinge, blir sidokraften 0, vilket man ser på din andra bild.

*om inte föraren har möjlighet att förflytta hela sin kropp långa sträckor i sidled. Ungefär som en "foiling moth".

Ett annat sätt att se på detta är att betrakta en enkel motorcykel där tyngdpunkten ligger i centerlinjen, och vingen verkar längs centerlinjen. Oavsett hur mycket kraft vingen ger, kan inte motorcykeln åka fortare i kurvan.

Jag ska se om jag kan sätta mig och räkna imorgon.

Men det verkar ju som att hela missförståndet ligger i hur motorcykeln definieras. Min definition är att burkningen är fast, medan lutningsvinkeln är variabel. Medan din definition verkar vara att lutningsvinkeln är fast, medan burkningen är variabel.

 

[Two stroke man]

Bearing, jag har hela tiden försökt få fram att du blandar in egna tankar som inte har med saken att göra.

Endast vingen vinkel påverkar down force och alfa i min ekvation är därför motorcykelns lutning.

Var föraren sedan sitter är irrelevant för burkningens "lutning" har ingen påverkan på down force, burkningen är bara nåt som krävs för att du inte ska tippa omkull utåt i kurvorna. Vidare så korrelerar därför vinkeln på ekipagets masscentrum till 100% med utnyttjat grepp. Och det är antagligen det som förvirrar dig och du försöker räkna baklänges från fel håll.

Ja, det är en helt korrekt, f(u,alfa) = 0 gäller just precis i den lutningsvinkeln där vingen upphör att fungera och u(alfa) = tan(alfa) är den friktion som krävs för en önskad maximal lutningsvinkel. Precis som jag sagt flera gånger med exemplet u = 1, så slutar vingen vara funktionell och blir tvärtom kontraproduktiv efter 45 grader.