It´s a kind of magic
Det ligger i mina gener!
Kan Hr. Pizzabagare förklara varför alla pizzabagare svarar "Hej, varrsåågudd" i telefon när man beställer pizza? "Varsågod" säger man när man GER något, inte när man tar emot en beställning
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
It´s a kind of magic
Det ligger i mina gener!
Kan Hr. Pizzabagare förklara varför alla pizzabagare svarar "Hej, varrsåågudd" i telefon när man beställer pizza? "Varsågod" säger man när man GER något, inte när man tar emot en beställning

Kul tanke och väl presenterat men problemet uppstår nog när man antar att stegen blir en diagonal när n=oänligheten det vill säga jämför oändligt många steg med diagonalen. Oändlighet är ett begrepp som kan skapa mycket underliga effekter.
Vad är tex Oändligheten/Oändligheten ?
Det här är ju samma tankevurpa som att om man bara tar halva brödet så finns det alltid bröd kvar.
x = 0,99999..
10x = 9,999999..
9x = 9,9999999 - 0,9999999 = 9
x = 1
x = 0,99999
10x = 9,9999
9x = 9,9999 - 0,99999 = 8,99991
x = 8,99991/9 = 0,99999
Spelar ingen roll hur många nior man har efter kommat. Misstaget kallas trunkationsfel om jag kommer ihåg rätt. Dock alltid lika kul.
Nu kanske jag är ute och cyklar, men det är väl just när man har ett visst antal 9or som det blir fel, .999!=1, att det måste vara ett oändligt antal 9or?
T.ex.
0.333..... = 1/3 => 3x.333.... = 3(1/3) => .9999..... = 3/3 = 1
.999 * 10 = 9.99 (man förlorar en decimal vilket bara sker när man har ett ändligt antal decimaler)
Vilket medför att det blir 8.991 när man tar 9,99 - .999. Men om man istället har 0.999.... skulle det motsvara 9.99 - 0.99 = 9
Eller?
per definition är det ju 1 men vad är oändligheten/(oändligheten-1)?
x = 0,99999
10x = 9,9999
9x = 9,9999 - 0,99999 = 8,99991
x = 8,99991/9 = 0,99999
Spelar ingen roll hur många nior man har efter kommat. Misstaget kallas trunkationsfel om jag kommer ihåg rätt. Dock alltid lika kul.
Man kan göra samma sak om man tar roten ur 2 tillräckligt många gånger på en kalkylator eller i tex Excel och sen kvadrerar resultatet lika många gånger. Hur många gånger man måste göra för att det skall bli fel beror på hur många siffror kalkylatorn/Excel arbetar med.
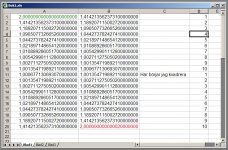
Liten snabb Excel koll
View attachment 323254
Börjar bli fel efter 10 gånger
Jag är ganska säker på att det blir som jag skrev. Excel och miniräknare är datorprogram och datorprogram kan inte skriva ett oändligt antal siffror utan måste klippa (trunkera) nånstans och då kan det bli fel ibland.
Exempelvis roten ur 2 har oändlig decimalutveckling så då tappar man ju information när man trunkerar och då kan det bli fel när man försöker sätta ihop det igen. I ditt excel-exempel så är ju roten ur 2 egentligen fel redan från början. Det ska inte vara en massa nollor på slutet utan det ska fortsätta med en massa andra siffror i all oändlighet.
Det är precis det jag sa tidigare.
"Misstaget kallas trunkationsfel om jag kommer ihåg rätt"
0,99 x 10 = 9,90
0,9999...99 x 10 = 9,999...990
0,9999.......................99 x 10 = 9,999.......................990
0,9999.................................99 x 10 = 9,999.................................990
Jo, fast det är ju bara brist hos datorprogrammet. Det säger ju inget om verkligheten. Fast det kanske var det som var din poäng. Isf missförstod jag dig.
Visst beror det på en "brist" i datorprogrammet, precis samma brist som ger dom kul effekterna i exemplen i den här tråden.
Jag tycker sådana här till synes förbryllande matematiska fel är skitkul men dom beror alltid på att man "trunkerar" eller hanterar oändligheten som ett vanligt tal.
Anta att det finns ett oändligt antal heltal. Mellan varje heltal finns det ju ett oändligt antal decimaltal.
Man kan ju då tycka att det ska finnas fler decimaltal än heltal, men hur kan det finnas fler än oändligt? Finns det olika oändligheter?
Anta ett filosofiskt perspektiv på det då.
Se oändligheten i heltalen som en yta, snarare än en sträcka. Se sen decimalerna som en sträcka i en cirkel (tänk CD-skiva) inom heltalens yta. Ju fler decimaler, desto mer komprimerade "spår".
???
<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Är inte oändlighet ett väldigt fabricerat begrepp? Och används inte "går MOT oändligheten" som term inom matten?
Det ger ju att den korrekta definitionen i sak inte alls är oändligheten, utan något så stort eller decimaliserat att vi uppfattar det som så. Och att skillnaden mellan vad som ÄR och vad vi UPPFATTAR är en del av definitionen.
Right?
Visst beror det på en "brist" i datorprogrammet, precis samma brist som ger dom kul effekterna i exemplen i den här tråden.
Jag tycker sådana här till synes förbryllande matematiska fel är skitkul men dom beror alltid på att man "trunkerar" eller hanterar oändligheten som ett vanligt tal.
Spelar ingen roll hur många nior man har efter kommat. Misstaget kallas trunkationsfel om jag kommer ihåg rätt. Dock alltid lika kul.

|
Nya Indian Pursuit Elite
Screenshot Indian Motorc... |
|
|
Icons of British Originality
Åtta team från åtta länder ... |
|

|
BMW presenterar R 12 G/S
BMW Motorrad har presentera... |

|
Europeisk kampanj för säkrare motorcykelkörning
Den europeiska branschorgan... |

|
BMW R 12 G/S
BMW Motorrad har presentera... |

|
Sveriges vägar i allt bättre skick
Foto: Liza Simonsson Utv... |

|
H-D Euro Festival i Port Grimaud 8-11 maj
Nu börjar det närma sig för... |

|
Norrtälje Custom Bike Show
Förra året firade Twin Club... |

|
Harley-Davidson Euro Festival närmar sig
8–11 maj smäller det – tiot... |

|
Sveriges vägar blir bättre
Foto: Samuel Unéus Utvec... |
