Motstyrningstråden 2.

[Lanson]

Härligt att det här tas upp det är inte många som vet om det! Jag gick nydligen på körskola men det var ingen som sa något om det till mig. men efter att ha läst och provat mig fram så är det ju solklart! Vrid styret åt vänster när du skall svänga höger

 

[2004erland]

Precis som elwe säger. Styr åt höger så tippar gyrokrafterna cykeln åt vänster. Det som sen styr cykeln är skillnsden i rullradie på däcket. Svänger man så har mitten på däcket större omkrets än den del av däcket som är mot kurvan. Denna skillnad i rullningsomkrets på hjulet får cykeln att svänga. Genom att motstyra under nerlägg så lägger sig cykeln mer och styr också mer. En cross styrs endast genom att man viker den under sig åt det håll man vill svänga. Erland.

 

[JTPK79]

...och jag har alltid trott folk sagt motorstyrning och tänkt, vad babblar de om. Tills idag, då jag läste mer noggrant och såg att det stod motstyrning

 

[kejsarn]

Har heller aldrig tänkt på detta, tror det sker per automatik efter ett tag. Dock aldrig resonerat som att jag styr tvärt emot, bara att jag styr mindre eller vad jag ska säga.
Bästa exemplet bör ju lämpligt vis vara speedway, det kallar jag motstyrning!

Får väl testa detta lite mer extremt när det blir dags för banåka igen, bli vår nu, snälla.

 

[roke]

Den allt överskuggande kraften vid snabba, exakta nedlägg kommer från gyrokrafterna utan att för den skull vara den enda verkande kraften.

Nja?
När det handlar om varför en mc lutar så säger Norrmännen som skrivit full kontroll:

Ett mycket mer exakt och effektivt sätt att få en kursändring är att ge ett kort frånskjut på styret på samma sida som du vill svänga åt. Denna rörelse, som kallas motstyrning, gör att framhjulet styr bort från den önskade svängens riktning. Framhjulets kontaktpunkt mot underlaget rör sig bort från linjen som resten av cykeln följer. Detta får motorcykeln att rotera runt sin egen tyngdpunkt, vilket gör att den lutar inåt i svängen. Fint, eller hur? Vi får också lite hjälp av gyrokrafterna i denna motsatta styrrörelse.

Gyroeffekten hjälper till att luta mc, men om jag förstått Norrmännen rätt så uppstår lutningen i huvudsak mest genom att framdäckets kontaktpunkt mot vägen rör sig bort från linjen som resten av cykeln följer.

Klippt härifrån:http://vulcanrider.se/Articles/FULL_KONTROLL_SVENO.pdf

 

[elwe]

Nja?
När det handlar om varför en mc lutar så säger Norrmännen som skrivit full kontroll:

Gyroeffekten hjälper till att luta mc, men om jag förstått Norrmännen rätt så uppstår lutningen i huvudsak mest genom att framdäckets kontaktpunkt mot vägen rör sig bort från linjen som resten av cykeln följer.

Klippt härifrån:http://vulcanrider.se/Articles/FULL_KONTROLL_SVENO.pdf

Ja, jag har läst denna skrift, eller rättare sagt gett den till min fru eftersom jag inte var av den åsikten att det fanns så mycket i den som jag inte redan provat eller visste, men tänkte att hon som nybörjare skulle kunna plocka upp något där som jag kanske glömt att tala om.
Jo, enligt citatet har du förstått norrmännen rätt när det gäller det de skriver, men det är min åsikt att de har fel när det gäller fördelningen mellan de olika krafterna och just när det gäller mekanik så baserar jag inte mina ståndpunkter på vad smc skriver utan hellre på egen utbildning och erfarenhet.

 

[Sladjan R1]

Den här tråden har säkert gett en hel del folk goda tips och råd, men jag undrar hur fan man klarar uppkörningen om man inte vet vad motstyrning är!!!???

Handlar inte en del av uppkörningen (undanmanöver) just om motstyrning? Jag vet inte vilket annat sätt man skulle kunna tänka sig att göra en undanmanöver på om inte just MOTSTYRNING.

Undantaget är alla "gubbar" som fick kortet på köpet när de tog B-kort, men om de inte har praktiserat MOTSTYRNING under sina 90 år bakom styret så.....

 

[roke]

Ja, jag har läst denna skrift, eller rättare sagt gett den till min fru eftersom jag inte var av den åsikten att det fanns så mycket i den som jag inte redan provat eller visste, men tänkte att hon som nybörjare skulle kunna plocka upp något där som jag kanske glömt att tala om.
Jo, enligt citatet har du förstått norrmännen rätt när det gäller det de skriver, men det är min åsikt att de har fel när det gäller fördelningen mellan de olika krafterna och just när det gäller mekanik så baserar jag inte mina ståndpunkter på vad smc skriver utan hellre på egen utbildning och erfarenhet.

Jo, det förstås, många av mina ståndpunkter i ämnen som jag tycker jag behärskar är också sprungna ur min egen erfarenhet och av vad jag lärt.

Men i fallet med varför en motorcykel lutar när man motstyr så tror jag på boken. Som för övrigt inte smc har skrivit? (som om inget bra kom ur smc?)
Jag kan till och med tänka mig in i, och begripa förklaringen, som säger att mc lutar därför att framdäckets kontaktpunkt lämnar linjen som mc följer.
Att gyrokrafterna hjälper till att tippa står ju också där.

 

[mudder]

....Gyroeffekten hjälper till att luta mc, men om jag förstått Norrmännen rätt så uppstår lutningen i huvudsak mest genom att framdäckets kontaktpunkt mot vägen rör sig bort från linjen som resten av cykeln följer..............

Precis. Ett enkelt sätt att illustrera hur en hoj kan balanseras eller lutas är att ställa ett kvastskaft i handflatan. Flyttar man undersidan åt vänster så faller skaftet åt höger. Testa detta nu och skit i gyroeffekten.

Det är helt enkelt så att hojen balanseras genom att flytta anliggningspunkten mot marken.

 

[Dan_the_man]

De flesta gör det nog utan att tänka på det...

 

[elwe]

Precis. Ett enkelt sätt att illustrera hur en hoj kan balanseras eller lutas är att ställa ett kvastskaft i handflatan. Flyttar man undersidan åt vänster så faller skaftet åt höger. Testa detta nu och skit i gyroeffekten.

Det är helt enkelt så att hojen balanseras genom att flytta anliggningspunkten mot marken.

Har du hört talas om tyngdpunkter och labila jämviktslägen?

 

[Sladjan R1]

De flesta gör det nog utan att tänka på det...

Onanerar?

 

[ft]

Eftersom du inleder en kvasivetenskaplig diskussion så får jag väl bemöta dig.

Ingen kvasivetenskap från mig, det är ren naturvetenskap.

1) Vid låg fart kan du fortfarande styra och balansera en hoj. Då är de gyroskopiska krafterna helt garanterat försumbara.

2) Om de gyroskopiska krafterna var av signifikant betydelse skulle hojens nerläggsvinkel ändras till stor del genom ett moment runt längdaxeln applicerat i framhjulets nav. Med de korta momentarmar som utgörs av hjulaxeln skulle vi prata om rejält höga krafter. Tänk dig själv att ersätta framhjulet med en kort stav och sedan kasta hojen från fullt nerlägg åt ena hållet till fullt nerlägg åt andra hållet på det sätt som görs i ett ess - enbart genom att vrida på den staven. Att du skulle få se lite intressant beteende från gaffeln och hjulaxelinfästningarna är ganska uppenbart. Därmed är det lika uppenbart orimligt att de gyroskopiska krafterna är av betydelse.

Sen kan man ju fundera lite på vad motsvarande gyroskopiska moment från bakhjulet skulle göra åt det hela... men det tar vi i nästa iteration.

3) En sak är säker: Det gyroskopiska momentet framhjulet skapar runt längdaxeln kommer att vara mindre än det moment du applicerar kring styraxeln. Mindre eftersom styraxeln inte är helt vertikal.

Detta ger ett kul litet tankeexperiment. Tänk att du hade styret fastsatt på andra ledden, d v s på höjden, och att du istället för att påverka styrändarna framåt/bakåt påverkar dem höger/vänster, med samma krafter som du använder för att manövrera din motorcykel. Givetvis förutsätter detta tankeexperiment ett mothåll som inte är fixerat vid motorcykeln.

Jämför detta med hur fort du går från höger till vänster nerlägg i ett ess. Kommer det moment du använder på styret att baxa runt över tvåhundra kilo hoj plus förare med de vinkelaccelerationerna? Kommer det ens att komma i närheten?

Är du inte Hulken och regelmässigt knäcker sönder styrkronor vid snabba växlingar av svängriktning så är svaret nej, nej och åter nej.

Om du färdas rakt fram med sparkcykel, skidcykel eller liknande och vrider på styret så påbörjar du att åka i en cirkelbåge och centrifugalkraften gör att fordonet vill välta utåt.

Gör man så är man en idiot och kan inte cykla. Kan man cykla gör man rätt (medvetet eller omedvetet), och gör man rätt på en sparkcykel, skidcykel, motorcykel, pedalcykel eller liknande så motstyr man och flyttar på så sätt stödpunkten medan tyngdpunkten, genom massans inneboende tröghet, förblir på samma ställe. Därefter skapas en lateral kraft genom friktion mot underlaget (skidor fungerar lite annars, men låt oss kalla det friktion - principen är i det här sammanhanget precis densamma) och en stabil sväng med nerlägg erhålls. Precis samma princip, och med noll till väldigt ringa inverkan av gyroskopiska moment.

Du skriver: "Man kan räkna på de gyroskopiska krafterna och komma fram till att det inte är en faktor... men det är jobbigt."
Jag skulle nog vilja påstå att det är jävligt jobbigt, iaf om du har ambitionen att utföra dessa beräkningar matematiskt och fysiskt oantastligt, men presentera gärna beräkningarna så vi kan gå igenom hur du tänker.

Näe, inte jävligt jobbigt. Bara jobbigare än att konceptuellt visa på det orimliga i det påstående du något okritiskt återger.

Kolla in den här länken. Där finns även den exakta beräkningen. Helt plötsligt är det inte jobbigare än att använda en miniräknare. Ha det så kul.

http://www2.eng.cam.ac.uk/~hemh/gyrobike.htm

Precis. Ett enkelt sätt att illustrera hur en hoj kan balanseras eller lutas är att ställa ett kvastskaft i handflatan. Flyttar man undersidan åt vänster så faller skaftet åt höger. Testa detta nu och skit i gyroeffekten.

Det är helt enkelt så att hojen balanseras genom att flytta anliggningspunkten mot marken.

Svårare än så är det faktiskt inte, hur mycket somliga än försöker trassla till det.

Bästa exemplet bör ju lämpligt vis vara speedway, det kallar jag motstyrning!

Eller inte.

När man börjar köra med sladd blandar man in en massa andra intressanta faktorer genom att en betydande del av bakdäckets sidkraft blir parallell med färdriktingen. Samtidigt riktas en rejäl del av den kraft som det spinnande bakdäcket genererar inåt i svängen för att täcka upp för det faktum att det inte finns grepp nog för att genom konventionella metoder ta sig runt svängen i den farten.

Enkelt uttryckt använder man motoreffekten (som skyfflar kolstybb och därmet skapar en kraft i däckets längdriktning) för att hjälpa friktionen på traven när friktionen inte längre räcker till.

Skall villigt erkänna att jag inte helt har förstått hela dynamiken bakom en sladdande tvåhjuling och hur den balanseras. Det är betydligt mer komplicerat än i det triviala fallet där vi inte blandar ihop driv- och bromskraft i längdled med friktionskraft i sidled...

 

[Niklasinorr]

När man börjar köra med sladd blandar man in en massa andra intressanta faktorer genom att en betydande del av bakdäckets sidkraft blir parallell med färdriktingen. Samtidigt riktas en rejäl del av den kraft som det spinnande bakdäcket genererar inåt i svängen för att täcka upp för det faktum att det inte finns grepp nog för att genom konventionella metoder ta sig runt svängen i den farten.

Enkelt uttryckt använder man motoreffekten (som skyfflar kolstybb och därmet skapar en kraft i däckets längdriktning) för att hjälpa friktionen på traven när friktionen inte längre räcker till.

Skall villigt erkänna att jag inte helt har förstått hela dynamiken bakom en sladdande tvåhjuling och hur den balanseras. Det är betydligt mer komplicerat än i det triviala fallet där vi inte blandar ihop driv- och bromskraft i längdled med friktionskraft i sidled...

En hoj som sladdar balanseras av sig själv tack vare motstyrning. När hojen sladdar så vrider den sig själv runt styrhuvudet så att motstyrning uppstår, men åt det håll som motverkar sladden dvs den styr tillbaka hojen i ett balanserat läge. Samma princip som när vi cyklar utan att hålla i styret

Jag var ute för en stund sedan med trampcykeln för att testa det här med motstyrning i låg fart. Jag försökte styra som med bilen, dvs medstyrning men jag klarade inte av det. Precis som den lilla killen på filmen i början av tråden, hans sväningar med styret är på grund att han motstyr, inte medstyr som man kan tro. Till och med när jag leder cykeln så gör jag en liten motstyrning innan jag vrider in styret i kurvriktningen, vilket får folk att tro att dom medstyr.

En tvåhjuling kan bara motstyras när man skall svänga, oavsett fart. Och när det går fort, riktigt fort, så vill en motorcykel inte svänga alls pga av den kraftiga gyrokraften, om man då inte tar i ordentligt med motstyrning så svänger man inte, så enkelt är det.

 

[anders_69]

Kolla in den här länken. Där finns även den exakta beräkningen. Helt plötsligt är det inte jobbigare än att använda en miniräknare. Ha det så kul.

http://www2.eng.cam.ac.uk/~hemh/gyrobike.htm

Svårare än så är det faktiskt inte, hur mycket somliga än försöker trassla till det.

En gammal professor i Lund har också utrett vad som har resp inte har betydelse för balansering av cykel, ex i denna utmärkta samling slides.
http://www.control.lth.se/~kja/Lectures/BikeTalkKTH2006.pdf

För att få ut nåt av beräkningarna krävs nog dock att man har minst motsvarande grundläggande kurs i reglerteknik för civilingenjörer, men det finns fina bilder att titta på annars.


En av slutsatserna är iaf att gyroeffekter har liten betydelse för balans/styrning.

 

[sTf_paPs]

"Gyro" krafterna har nästan ingen betydelse alls. Det som händer när man motstyr år att hojens geometri gör så att hojens tygndpunkt hamnar utan för linjen mellan hjulens kontaktpunkter.

Man vill svänga till höger och då vill man luta hojen åt höger.

Vrid styret åt vänster så händer följande



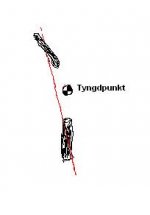
Hojens tyngdpunkt hamnar till höger om kontaktlinjen och detta får hojen att luta höger.

Motstyrning = hojens vikt plus din vikt vill luta hojen innåt medan masströgheten vill räta upp den = lätt att lägga ner och svänga.

Medstyrning = Din vikt (om du inte hänger av satan), masskrafter och hojens vikt vill luta hojen utåt i kurvan = krash.

Detta gäller även för cyklar och moppar och alla motstyr utan att veta om det så fort man lärt sig cyckla.

Tyvärr upphör ofta denna naturliga grej när man hamnar i trängda situationer.

"Typfallet"

Man påbörjar en kurva med "perfekt" motstyrning vilket leder till ett just nedlägg men till sin fasa upptäcker man att det går för fort och att man är på väg att drifta ut i mötande fil (eller diket). Vips börjar hjärnan arbeta och säger bromsa och sväng i vägens riktning för i helvete din idiot. Givetvis lyssnar man på hjärnan i detta ögonblick och det ger som resultat att hojen rätar upp sig och går rakt fram.

Nä träna in motstyrning så att det sitter som en pingissmash. Man hinner inte tänka utan det är en reflex.

Jag är ingen (fartfantom) hejare på detta själv men jobbar på det. Det lilla jag kan har dock räddat mig några gånger.

 

[freding]

Men är detta så viktigt?

När man börja med moppe brydde man sig inte överdrivet mycket åt teorin i körtekniken. Sen har det rullat på och man kör som man alltid gjort. Jag hade inte innan den förra tråden tänk eller brytt mig om detta. Inte heller lagt nån vikt på det efter heller, och jag tycker jag klarat mig bra utan. Kör ju faktisk hyfsat fort.

OM du inte vet vad och varför du gör för att åstadkomma det du är ute efter...hur ska du då veta vad du ska förbättra när du vill bli snabbare? Kan ju vara gott att speeda upp "trial and error metoden" lite

 

[Jonte]

OM du inte vet vad och varför du gör för att åstadkomma det du är ute efter...hur ska du då veta vad du ska förbättra när du vill bli snabbare? Kan ju vara gott att speeda upp "trial and error metoden" lite

Oj hur gammalt var mitt inlägg? Visst fundera jag hur jag skulle förbättra tekniken när jag tävlade men nu handlar det mer om mod.

 

[Ravetrancer]

Men vad är det här för jävla tråd? Att köra båge sitter ju för h-e i ryggmärgen. Sitter alla och tänker på vad dom gör när dom kör eller?

Näe..vänta nu..eeeh..i med kopplingen först..eehh..sen..putta till växelväljaren..ee..vad var det sen..eeh?. Ska jag vrida styret åt vänster eller höger??

Cykeln är ju bara en del av ens kropp typ när man kör. Vet inte om det är för att man har kört sen man var 6 år som man tycker att allt är självklart men har man verkligen på två hjul att göra om man sitter och tänker på grejer som borde komma automatiskt?

saken är att alla kan köra ändå, men när du vet om hur det funkar så kan du hantera hojen på ett helt annat sätt, medvetenhet om saker man gör är bra. På detta sätt så är du medveten om vad du gör och har mer kontroll över det.
Hjälpte definitivt mig att bli snabbare på tiden man fick på sig ett skinnställ iaf.

 

[SKOMAKARN]

Men vad är det här för jävla tråd? Att köra båge sitter ju för h-e i ryggmärgen. Sitter alla och tänker på vad dom gör när dom kör eller?

Näe..vänta nu..eeeh..i med kopplingen först..eehh..sen..putta till växelväljaren..ee..vad var det sen..eeh?. Ska jag vrida styret åt vänster eller höger??

Cykeln är ju bara en del av ens kropp typ när man kör. Vet inte om det är för att man har kört sen man var 6 år som man tycker att allt är självklart men har man verkligen på två hjul att göra om man sitter och tänker på grejer som borde komma automatiskt?

Precis detta tänkte jag åxå! Man lär sej cykla när man är, typ, 3-6 år. Sen kör man! Motstyrning o motstyrning, KÖR BARA